Funciones

Qué es una función?

Una función es una relación entre un conjunto de entradas y conjunto de posibles salidas donde cada entrada está relacionada exactamente con una salida.

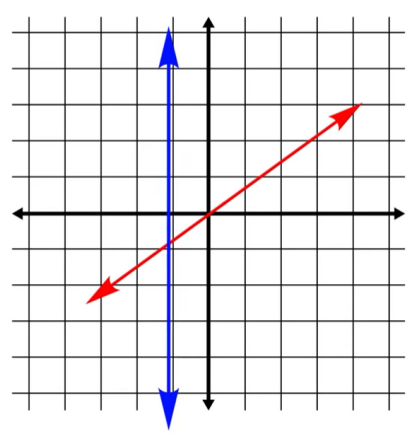
una línea vertical solo puede intersectar la función en un punto en un momento dado

és una función

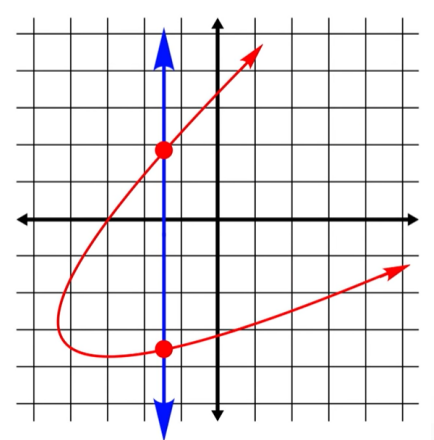
si una recta vertical se corta en dos o más puntos NO es una función

NO és una función

Dominio y Rango

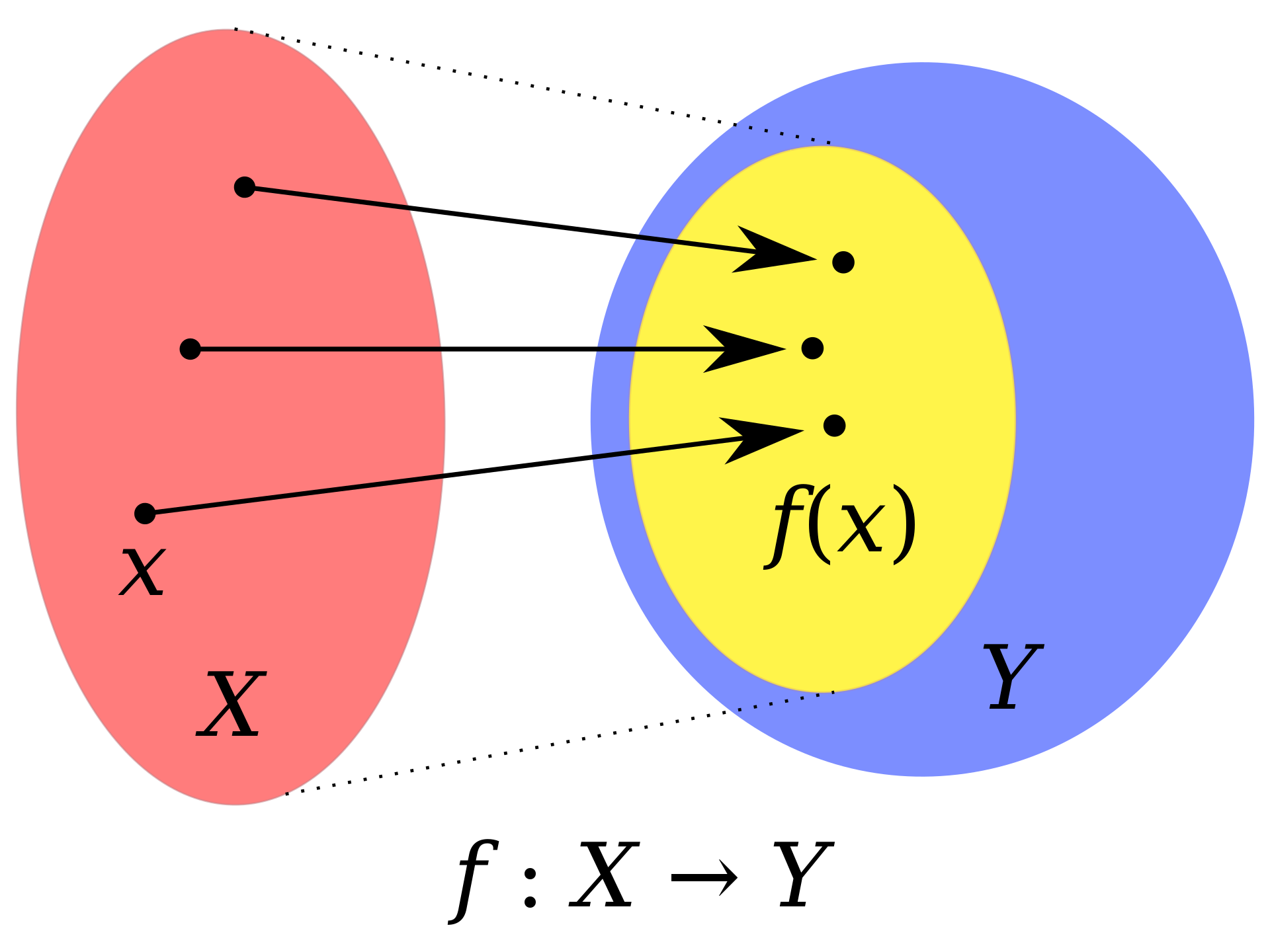Ilustración que muestra f, una función con dominio X y codominio Y. El óvalo pequeño dentro de Y es la imagen de f, a veces llamado rango de f.

Dominio

El dominio son los posibles valores de X que pueden ser insertados en la función

\[todos-los-números-reales \to f(x) = 2x + 1 \to todos-los-números-reales\]

Rango

El rango son los valores que la función puede tener

\[todos-los-números-reales \to f(x) = \left| x \right| \to [0, \infty]\]

Ceros en una función

Los ceros en una función son las intersecciones de X en el gráfico de esa función.

(y = 0)

Diferentes tipos de funciones darán lugar a diferentes numero de ceros en esa función.

Evaluar una función

Simplemente tenemos que insertar el valor que queramos evaluar a la función

Por ejemplo tenemos esta función:

\[f(x) = 3x^2 - 5x + 2\]

Pues para evaluar el 2 en esa función tenemos que substituir la x por 2:

\[f(2) = 3(2)^2 - 5(2) + 2\]

También podemos substituir la X por expresiones algebraicas

\[f(x) = 2x + 1\] \[f(x + 3) = 2(x + 3) + 1 = \textbf{2x + 7}\]

Manipular funciones