Autores
- Marta Jover Valero
- Mario Dorado Martínez
Introducción
Hemos decidido analizar el videojuego The Legend of Zelda: Breath of the Wild, ya que uno de sus grandes logros, es haber creado un sistema de físicas bastante elaborado que interactúa entre sí.
Este sistema contempla que los metales son conductores, por tanto, si utilizas elementos metálicos como espadas, escudos, etc., puedes crear una suerte de cables para así resolver puzzles.
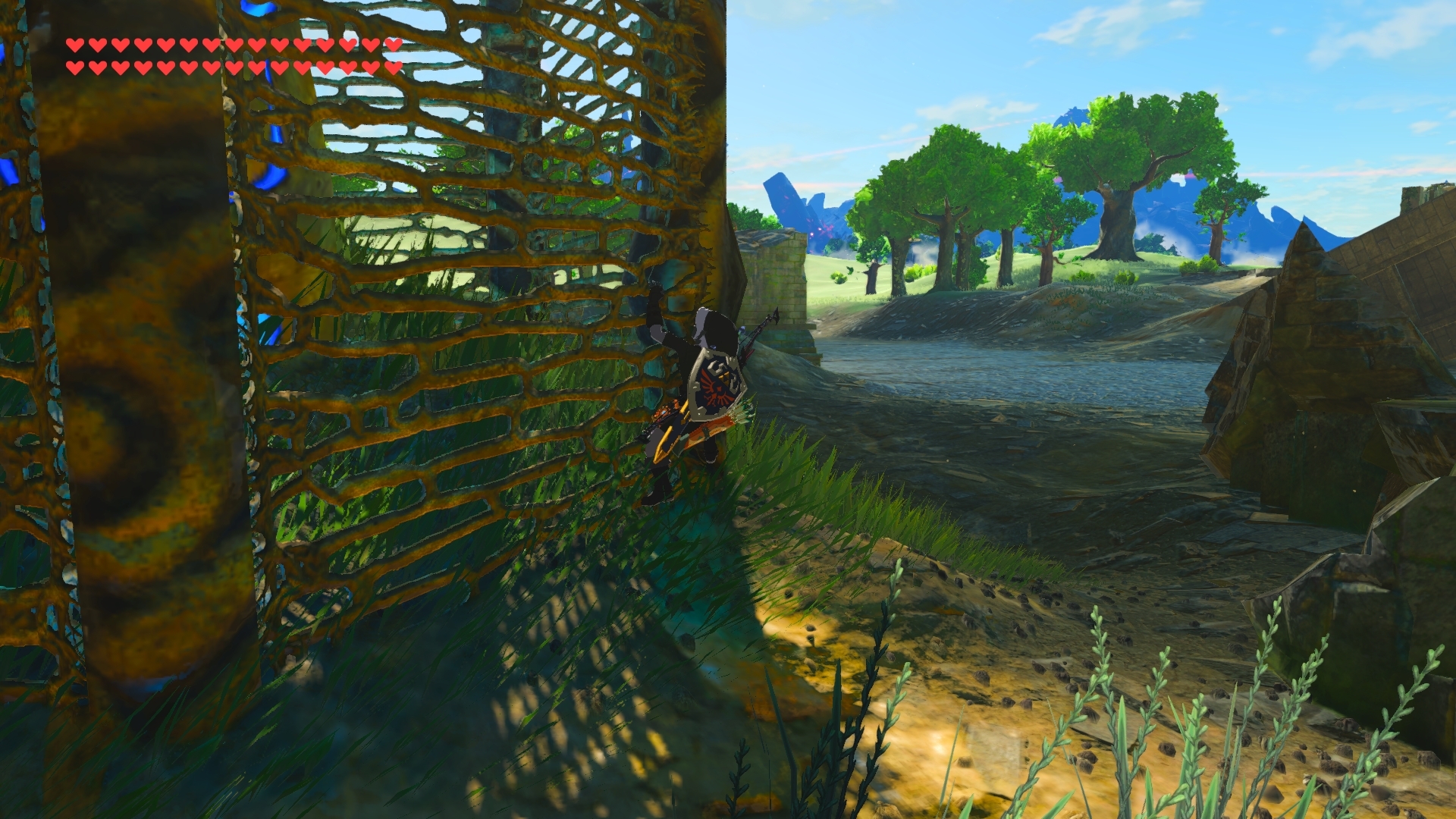
Ejemplo de como un jugador resuelve un puzzle de forma alternativa utilizando armas y armaduras como elementos para conducir la electricidad
También, los objetos tienes propiedades físicas básicas. Por ejemplo, si están en una tabla y esa tabla es empujada por un objeto pesado, los objetos salen despedidos.
BotW physics in a nutshell #BreathoftheWild #NintendoSwitch pic.twitter.com/o341FlzcpI
— Pinwheel Popper (@PinwheelPopper) August 15, 2019
Otro ejemplo que nos hemos encontrado mientras grabábamos el material necesario para el análisis, es que si disparas una flecha contra piedra, la flecha queda suelta en el suelo. Las ráfagas de viento las hacen rodar, y si es disparada contra una superficie en la que hay tierra o césped, la flecha queda clavada evitando el movimiento.
En el juego puedes encontrar diferentes minijuegos, uno de ellos inspirado en los bolos. En este podemos ver las físicas de la bola de nieve cayendo por el acantilado. Va cogiendo velocidad poco a poco hasta derribar las columnas de madera a partir de la fuerza que ha tomado en la caída. Este minijuego es muy curioso porque según en que punto tires la bola de nieve, no tiene la fuerza suficiente para derribarlos todos, así que lo hemos considerado un punto muy positivo para elegir Breath of the Wild como nuestro ejemplo para el proyecto.
Como hemos tomado medidas
Para tomar las medidas para realizar los cálculos, henos cogido como referencia un elemento del cual sabemos el tamaño, en este caso, tomamos la estatura del protagonista del juego; Link, la cual es de 1.70 metros.
Gracias a este dato y a las capturas que hemos ido tomando dentro del juego, hemos ido colocando al personaje repetidas veces sobre las superficies que queríamos medir utilizando el programa Photoshop.
De esta forma hemos obtenido unas distancias aproximadas. Y de forma colateral, hemos creado una nueva unidad para medir longitudes, el Link
Para los tiempos, hemos grabado videos realizando las acciones a analizar y posteriormente, utilizando programas de edición de vídeo, colocado temporizadores los cuales nos sirven para ver de forma bastante precisa cuanto tiempo transcurre durante, por ejemplo, un disparo con arco.
Caída libre
Primero de todo, hemos analizado una caída libre lanzando al personaje de Link desde una torre, así podremos saber la gravedad que hay dentro del videojuego y ver si es un valor realista.
Comparativa de tamaño entre Link y la torre
Al ser una caída libre, hemos utilizado la fórmula del MRUA, ya que es un movimiento acelerado por la gravedad.
Tiempo en el juego
\[X(t) = X_{0} + v_{0}t + \frac{1}{2} \cdot at^{2}\] \[0 = 78.2 + 0 + \frac{1}{2} \cdot 2.152 \cdot a^{2}\] \[a^{2} = \frac{-78.2 - \frac{1}{2}}{2.152} = -33.83\]Haciendo los cálculos, podemos observar que la fuerza de la gravedad es de unos -33.83 m/s2 o -19.9 links/s2, lo cual es un valor muy superior al de la tierra (9.8 m/s2), esto significa que, en el mundo de The Legend of Zelda: Breath of the Wild, hay más gravedad que en Júpiter (24.79 m/s2).
Tiempo en la vida real
Haciendo los cálculos con la gravedad que tenemos en el planeta tierra, podemos obtener el tiempo que tardaría Link en caer desde lo alto de la torre hasta el suelo y ver la diferencia con los tiempos que hemos medido dentro del juego.
Utilizamos la fórmula del MRUA:
\[X(t) = X_{0} + v_{0}t + \frac{1}{2} \cdot at^{2}\] \[0 = 78.2 + 0 + \frac{1}{2} \cdot t \cdot 9.81^{2}\]Haciendo los cálculos, obtenemos que una caída de la misma altura con unos valores de gravedad realistas (9.81 m/s2), la caída duraría unos 3.99 segundos, lo cual queda en una diferencia de tiempo de 1.90 segundos.
Tiro parabólico
Para analizar que factores físicos tiene en cuenta el videojuego a la hora de realizar un tiro parabólico, hemos disparado una flecha con un arco.
Para calcular el tiro parabólico, necesitamos saber el ángulo en el cual sale disparada la flecha, cuanto tiempo tarda en impactar contra el suelo y a cuanta distancia impacta.
Para obtener el ángulo con el que sale la flecha, hemos cogido la imagen dónde se ve la trayectoria de la flecha con su respectiva parábola y dibujamos un triángulo aproximado para sacar sus ejes y calcular las distancias a partir de los píxeles de largo y alto que ocupan.
Una vez colocados los ejes, cogemos la longitud del eje X y del eje Y, buscamos la tangente:
\[\tan (\alpha )=\frac{sin(\alpha )}{cos(\alpha )}\]Y a partir del resultado, buscamos el arcotangente.
\[\alpha =\arctan (tan(\alpha ))\]De esta forma, sacamos de forma aproximada el ángulo de la parábola.
Para saber cuanto tiempo tarda en impactar contra el suelo, hemos disparado la flecha y cronometrado cuanto tiempo tarda en caer al suelo.
Para medir la distancia que ha recorrido la flecha, hemos hecho una captura colocando el personaje desde la posición que se ha disparado la flecha, y otra dónde ha impactado la flecha, y utilizando al personaje como forma de medida, hemos sacado la distancia.
Parábola que realiza la flecha al ser disparada
Al final, con todos estos valores obtenemos que la flecha es disparada con unos 14.3 grados de inclinación y recorre 64.6 metros en 1 segundo.
A continuación, vamos a descomponer el vector velocidad en dos componentes: velocidad horizontal y velocidad vertical.
Para calcular la velocidad horizontal, tenemos que dividir la distancia que recorre la flecha entre el tiempo que tarda en recorrerla. Esto es así, ya que asumimos que es una velocidad constante, ya que al ser una flecha, la fricción con el aire es mínima.
\[\frac{64.6}{1} = 64.6\]Esto nos da como resultado que la flecha tiene una velocidad horizontal de 64.6 m/s o 38 links/s.
\[V_x = \left | V \right |\cdot \cos\alpha\] \[V_y = \left | V \right |\cdot \sin\alpha\]Substituimos el módulo por la velocidad horizontal.
\[V_y = (\frac{V_x}{\cos\alpha}) \cdot \sin\alpha\]Relación trigonométrica sin α / cos α = tan α
\[V_y = V_x \cdot \frac{\sin\alpha}{\cos\alpha}\] \[V_y = V_x \cdot \tan\alpha\] \[V_y = 64.6 \cdot \tan 14.3^{\circ} = 16.47m/s\]Esto nos da que la velocidad vertical es igual a 16.47 m/s o 9.69 links/s.
Para calcular la gravedad, hemos utilizado la fórmula del MRUA, con la componente de velocidad vertical, ya que esta velocidad está influenciada por la aceleración que ejerce la gravedad, sin embargo, la horizontal no.
MRUA:
\[X(t) = X_{0} + v_{0}t + \frac{1}{2} \cdot at^{2}\] \[0 = 0.85 + 16.47 \cdot 1 + \frac{1}{2} \cdot a \cdot 1^{2}\] \[a = \frac{(-0.85) - (-16.47) \cdot 1}{1^{2} \cdot \frac{1}{2}} = 32.09 m/s^{2}\]*0.85 m = 0.5 links (altura inicial desde la que se lanza la flecha).
Obtenemos que, la fuerza de la gravedad es igual a: -32.09 m/s2 o -18.88 links/s2, que es un valor bastante similar al que hemos calculado previamente en la caída libre. Podemos asumir que el juego tiene un único valor para la gravedad, y que la diferencia entre los valores es debida a errores de medida.
Catapulta
Utilizando varios elementos que encontramos sueltos por el mundo de Breath of the Wild, podemos crear fácilmente una suerte de catapulta. Hemos querido ver cómo de fidedignas son las físicas comparándolas con la vida real.
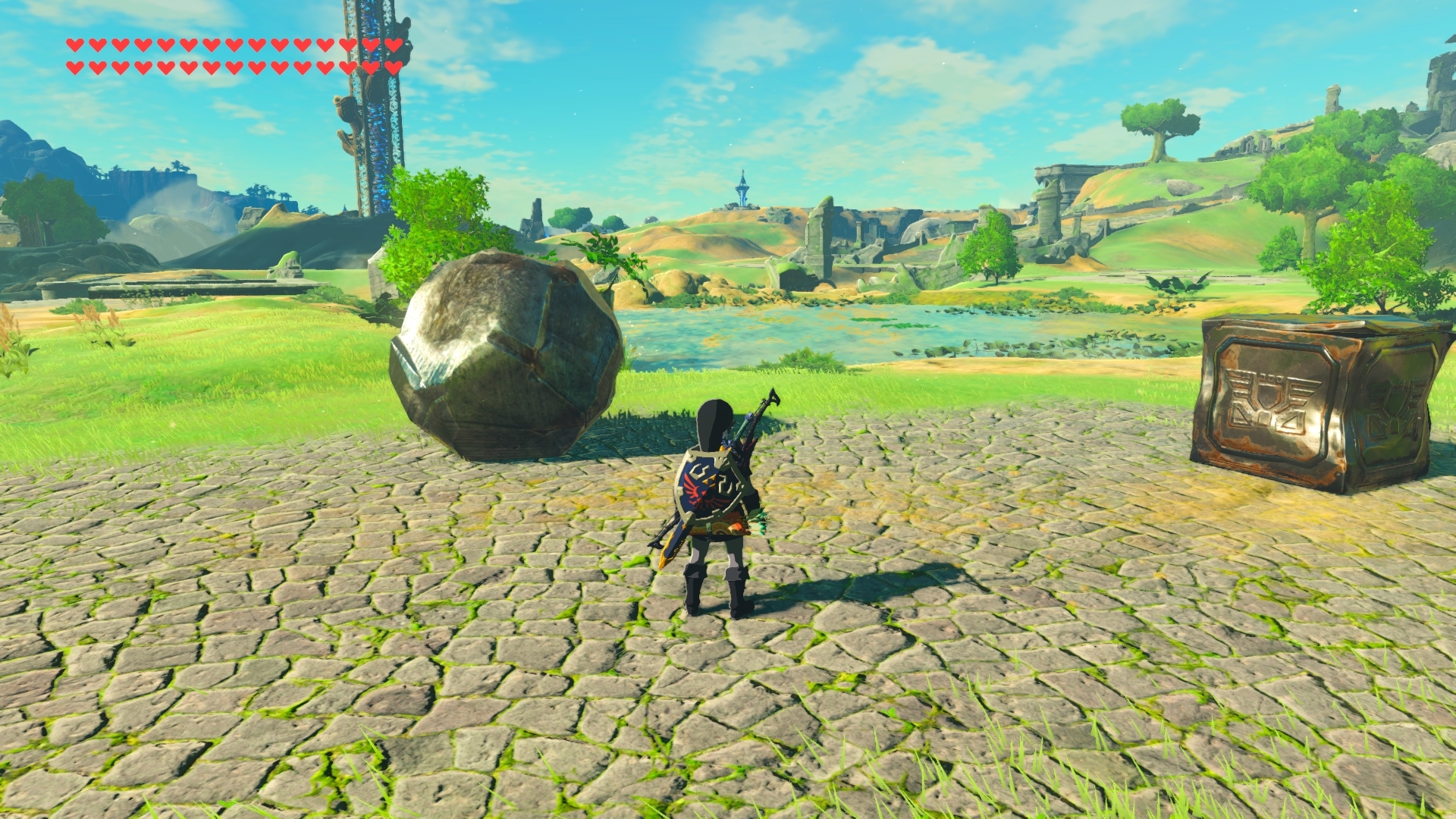Materiales para utilizados para crear la catapulta
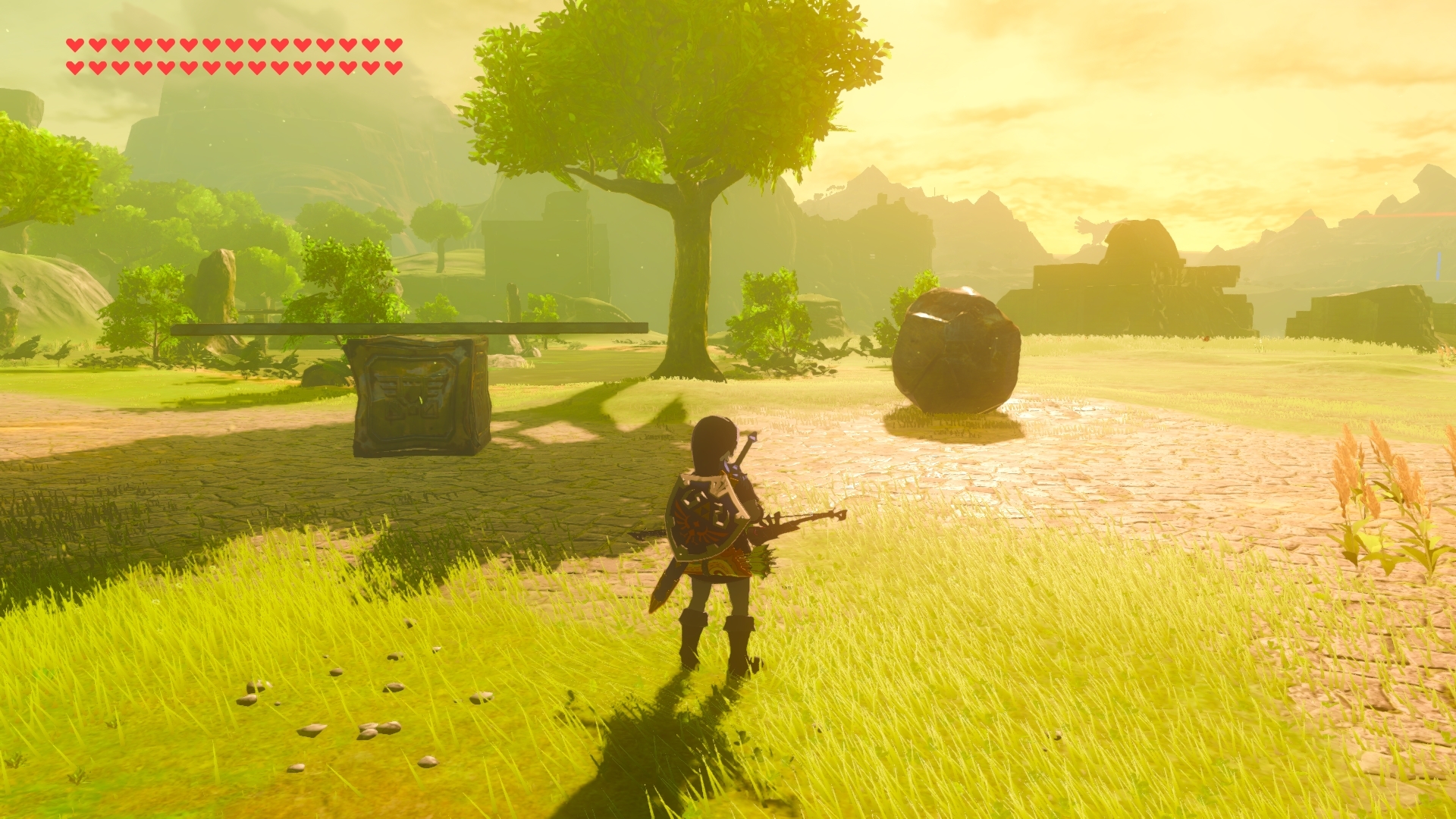Imagen de la catapulta desde cerca
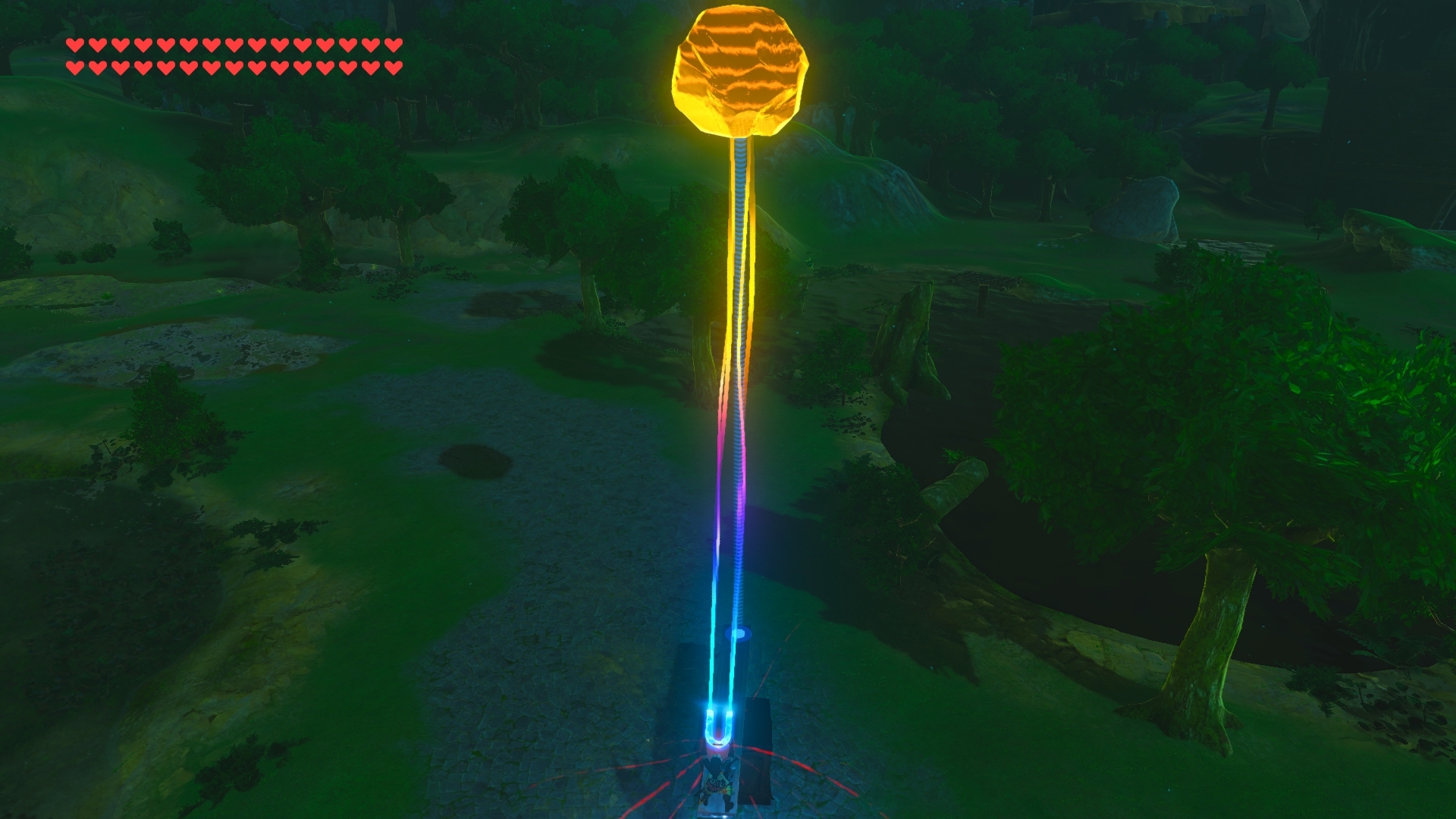Perspectiva del jugador antes de soltar la piedra
Primero, necesitamos saber la velocidad a la que sale despedido Link, teniendo en cuenta los valores de la gravedad, el tiempo que tarda en caer y la posición inicial.
Para conseguir la velocidad inicial que adquiere Link al ser lanzado, vamos a utilizar la fórmula del MRUA:
\[X(t) = X_{0} + v_{0}t + \frac{1}{2} \cdot at^{2}\] \[0 = 2.55 + v_{0} \cdot 2.44 + \frac{1}{2} \cdot (-33.34) \cdot 2.44^{2}\] \[V_{0} = 93.32 m/s\]Obtenemos que Link sale despedido a una velocidad de 93.32 m/s o 54,89 links/s.
El siguiente paso sería ver a cuanta fuerza es sometido Link durante el lanzamiento. Para esto necesitamos saber la masa de nuestro protagonista. Como no tenemos ninguna forma de medir cuanto pesa, hemos consultado en internet cuál es el peso promedio para un adulto varón de 1.70 metros de altura y asumimos que ese es el peso del personaje, el cual es de unos 65 kg.
Lo siguiente es medir cuanto tiempo tarda Link en salir despedido desde que la piedra impacta contra la tabla, es decir, el tiempo que Link está acelerando. Utilizando el vídeo anterior, vemos qué link se despega de la tabla 85 milésimas después de que la piedra impacte.
Dividiendo la velocidad inicial entre el tiempo que tarda Link en despegar, podemos calcular cuál es la aceleración.
\[\frac{93.32}{0.085} = 1097.88 m/s^{2}\]Lo cual nos da que Link acelera a una velocidad de, 1097.88 m/s2 o 645,81 links/s2.
Sabiendo la aceleración, podemos multiplicarla por la masa y así obtener la fuerza que recibe el personaje.
\[1097.88 \cdot 65 = 71.82kN\]Según la web Petzl España:
Este valor procede de estudios militares sobre paracaidistas: el cuerpo humano de un deportista podría soportar una deceleración máxima de unos 15 G, es decir, 12 kN para una masa de 80 kg.
Teniendo en cuenta que la piedra no da toda la energía justo cuando choca con la plataforma, sino que es entregada “linealmente” hasta que la tabla toca el suelo, no podemos saber la masa exacta de la piedra, pero podemos determinar la masa mínima. Esto lo podemos saber igualando la energía potencial de la piedra con la energía cinética de Link. Al hacer esto, sacaríamos la masa de la piedra si disipara toda su energía al contactar con la plataforma y no al contactar con el suelo.
Sabiendo la velocidad inicial, podemos calcular la energía cinética de Link.
\[\frac{1}{2} \cdot mv^{2}\] \[\frac{1}{2} \cdot 65 \cdot 93.32^{2} = 283.03kJ\]Para la altura hemos cogido la altura total, porque, si pusiéramos la altura total menos la altura de la plataforma, estaríamos diciendo que toda la energía se transfiere cuando la piedra toca la plataforma, pero, eso no es verdad. Así que asumimos que la energía es transferida de forma uniforme mientras la piedra empuja la plataforma y que transfiere toda la energía cuando toca el suelo.
Teniendo en cuenta esto, podemos decir que esto es una aproximación asumiendo que toda la energía de la piedra fuera transferida a Link, lo cual es mentira, porque en el vídeo se aprecia que la piedra aún tiene energía al contactar con suelo. Así que estos cálculos serían una cota inferior.
\[Ep = m \cdot g \cdot h\] \[m \cdot \left | -33.34 \right | \cdot 17.85 = 283.03kJ\] \[m = \frac{283030}{\left | -33.34 \right | \cdot 17.85} = 475.59kg\]Podemos ver que, 475.59 kg es la masa mínima que tendría que tener la piedra para disparar a Link a esa velocidad.
Para comprobar si en el juego, se conservan las energías, hemos mirado la energía potencial en el punto máximo de altura y la hemos comparado con la energía cinética que tiene Link al ser lanzado.
\[Ep = m \cdot g \cdot h\] \[Ep = 65 \cdot \left | -33.34 \right | \cdot 21.7 - 2.55 = 47.02kJ\] \[283.03 - 47.02 = 236.01kJ\]Haciendo estos cálculos, podemos observar que hay una pérdida de energía de 236.01 kJ, lo cual no es realista, ya que la energía es una magnitud conservativa. No sabemos cual puede ser el factor por el cuál perdemos tanta energía, ya que la fricción con el aire no debería disiparla tanto.
Habiendo analizado todos estos parámetros, podemos decir que las físicas del videojuego son bastante dispares con las físicas reales.
Salto de Link
Teníamos curiosidad sobre si el juego tenía en cuenta el peso de Link a la hora de calcular las físicas dentro del juego. Para comprobar esto, hemos capturado dos vídeos del personaje saltando con una armadura y sus armas equipadas, lo cual aumentaría la masa que tiene que elevar Link a la hora de saltar, y otro salto sin nada. En teoría, Link debería saltar más sin tener nada equipado.
Medidas del salto de Link con armadura
MRUA:
\[X(t) = X_{0} + v_{0}t + \frac{1}{2} \cdot at^{2}\] \[0 = 0 + v_{0} \cdot 0.27 + \frac{1}{2} \cdot (-33.34) \cdot 0.27^{2}\] \[v_{0} = 0.95m/s\]Link, al saltar, tiene una velocidad inicial de 0.95 m/s o 0.56 links/s.
No podemos calcular la fuerza con la que salta Link, ya que la animación es instantánea, no podemos medir cuanto tiempo Link está acelerando.
Medidas del salto de Link sin armadura
Podemos observar que el videojuego no tiene en cuenta la masa de Link, ya que salta la misma altura cuando tiene equipada una armadura y sus armas que cuando no las tiene equipadas.
Webgrafía
¿Cómo se ha determinado la fuerza de choque máxima de 12kN? - Petzl España. (s. f.). https://www.petzl.com/ES/es/Sport/%C2%BFComo-se-ha-determinado-la-fuerza-de-choque-maxima-de-12kN-?ProductName=MAMBO-10-1-mm
Pinwheel Popper on. (2019, 15 agosto). Twitter. https://twitter.com/PinwheelPopper/status/1162063176520704001?s=20
Metal weapons Conduct electricity. (s. f.). Imgur. Recuperado 23 de diciembre de 2022, de https://imgur.com/miBXgFC
Breath of the Wild - Pondo Snowball Bowling Easy Setup for Strikes. (2017, 31 marzo). YouTube. Recuperado 23 de diciembre de 2022, de https://www.youtube.com/watch?v=D3FdJk9vwDA&feature=youtu.be
Lic. Marcela Licata - zonadiet.com. (s. f.). Tabla de Peso Ideal en metros y kilogramos. Zonadiet. https://www.zonadiet.com/tablas/pesoideal.cgi
Cemu Emulator. (s. f.). https://cemu.info
GitHub - etra0/botw-freecam: Freecam for the game Zelda: Breath of the Wild for the Wii U using the Cemu emulator. (s. f.). GitHub. https://github.com/etra0/botw-freecam
Wiki Targeted (Entertainment). (s. f.). The Legend of Zelda Wiki. https://zelda.fandom.com/es/wiki/Link
colaboradores de Wikipedia. (2022b, diciembre 23). Júpiter (planeta). Wikipedia, la enciclopedia libre. https://es.wikipedia.org/wiki/J%C3%BApiter_(planeta)